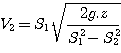
Théorème de Torricelli
On considère un récipient cylindrique de rayon R1 et de section S1 percé par un petit trou de rayon R2 et de section S2 contenant un liquide non visqueux. Soit z la hauteur verticale entre le trou B et la surface du liquide A.
Si R2 est beaucoup plus petit que R1 la vitesse du fluide en A est négligeable devant V, vitesse du fluide en B le théorème de Bernouilli permet d'écrire que :
PA - PB + m.g.z = ½mV².
Comme PA = PB (pression atmosphérique), il vient :

V = (2.g.z)^½.

La vitesse d'écoulement est indépendante de la nature du liquide.

Ecoulement d'un liquide par un trou
Si R2 n'est pas beaucoup plus petit que R1, la vitesse du fluide en A n'est plus négligeable. On peut alors écrire que S1.V1 = S2.V2 (conservation du volume). Du théorème de Bernouilli, on tire que :

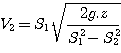
Comme la vitesse d'écoulement est fonction de z, elle n'est plus constante.
En écrivant la conservation du volume du fluide, on a : -S1.dz = S2.V2.dt. L'intégration de cette équation différentielle donne la loi de variation de la hauteur de liquide en fonction du temps.

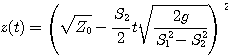
Cette relation n'est valide que si les conditions d'application du théorème de Bernouilli sont respectées.

 L'applet
L'applet simule l'écoulement d'un liquide par un trou cylindrique.
Les trois zones de texte permettent de choisir le rayon du réservoir, celui du trou et la hauteur de liquide initiale.
Pour lancer l'animation, il suffit de valider la dernière valeur entrée ou de cliquer sur le bouton [Départ].
En cliquant sur la souris (avec le curseur dans le cadre de l'applet), on gèle de façon temporaire l'animation.

Daniel BERNOUILLI (1700 - 1782) Physicien et mathématicien suisse.
Evengelista TORRICELLI (1608 - 1647) Physicien italien