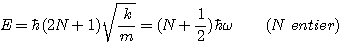
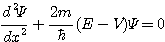
Le fait que y(x) soit un polynôme impose que les valeurs possibles pour l'énergie
sont données par :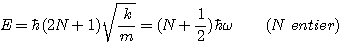
La particule ne peut être au repos : son énergie minimale est E = ½ h.w.
Pour un oscillateur harmonique classique, la probabilité de présence est
maximale pour les valeurs extrêmes de l'amplitude (vitesse nulle) et elle
est minimale pour une élongation nulle (vitesse maximale). Pour un oscillateur
quantique, les phénomènes sont très différents surtout pour les faibles valeurs
de N. Quand N augmente, on retrouve le fait que la probabilité de présence est
maximale au voisinage de X0 = ±(2N + 1)½ .
L'applet :
Les zones
de texte permettent de modifier les valeurs de la constante de rappel K et de
la masse M (les unités sont arbitraires).
Les traits bleus correspondent
aux niveaux d'énergie autorisés.
Les courbes en rouge représentent la probabilité
de présence de la particule. (Carré de la fonction d'onde). L'axe des abscisses est gradué en coordonnées réduites
X.
La parabole dessinée en noir correspond aux valeurs de X0 =
(2N + 1)½.