Oscillateur paramétrique
Commentaires :
On considère une aiguille aimantée de moment magnétique
m et de moment d'inertie J placée dans un champ magnétique
B = B0 + B1sin( wt ).
On pose K = B1 / B0 et w02
= mB0 / J. Si on prend en compte un amortissement visqueux, l'équation
qui donne l'angle q de rotation de l'aiguille s'écrit
:
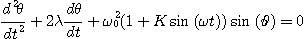 .
.
Un oscillateur dont le terme en sin(q) dépend
d'un paramètre de contrôle est un oscillateur
paramétrique. C'est un oscillateur non linéaire
dont le comportement peut être complexe et chaotique. L'équation
du mouvement n'admet pas de solution analytique et doit être intégrée
numériquement.
Ce dispositif permet de visualiser les problèmes posés par les
systèmes non linéaires et en particulier par leur grande sensibilité
aux conditions initiales et donc par la difficulté de leurs simulations
numériques.
L'applet
L'équation est intégrée numériquement
par une méthode de Runge-Kutta avec un pas que l'utilisateur peut modifier. La
vitesse initiale est toujours nulle.
Vérifier que pour B1
= 0, on retrouve un oscillateur harmonique : la trajectoire dans l'espace des
phases est une ellipse si l'amortissement est nul.
Selon les valeurs des paramètres
du système, on peut observer différentes situations.
Mouvement oscillant :
Prendre (par exemple) l = 0.15, q
initial = 30°, w0 / w
= 2.1, B1 / B0 = 0.4, pas = 0.02 s.
Le système oscille et tend vers un régime stable après
disparition du régime transitoire dont la durée est fonction de
l'amortissement (Faire varier l entre 0.05
et 0.5). Si l'on diminue w, l'amplitude du régiment
permanent croit jusqu'au moment ou le pendule décroche.
Accrochage : Faire varier B1 / B0 jusqu'à
la valeur 1.735 qui correspond à une bifurcation. Pour cette valeur,
l'aiguille tourne avec la fréquence de l'excitation (une vibration sinusoïdale
est la somme de deux vecteurs qui tournent en sens inverse). Une modification
même minime des conditions initiales (angle initial, valeur du pas d'intégration)
entraîne des modifications considérables dans le mouvement.
Chaos puis Mouvement oscillant : Prendre (par exemple) l
= 0.15, q initial = 30°, w0
/ w = 1.732, B1 / B0
= 0.4, pas = 0.02 s; Après des mouvements chaotiques, l'aiguille oscille
avec un mouvement sinusoïdal. Ici encore la sensibilité aux conditions
initiales est très grande.
Le programme affiche (en radians) les valeurs
extrêmes de q .
Ne pas omettre de valider la dernière
valeur saisie.
 Retour
au menu "mécanique".
Retour
au menu "mécanique".
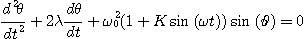 .
.