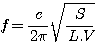
Résonateur de Helmoltz

 Un résonateur acoustique est une cavité de volume V ouverte par un tube de diamètre D (section S) et de longueur L. Si la longueur d'onde des ondes acoustiques est grande devant toutes les dimensions du résonateur, l'air contenu dans le tube se comporte comme un piston de masse m = mLS qui agit sur l'air contenu dans la cavité (constante élastique K).
Compte-tenu de la vitesse de déplacement de ce piston gazeux, on peut considérer que le phénomènes est adiabatique et si le déplacement du piston est x(t), on peut écrire :
p₀V^g = p(V - Sx)^g.
 Comme Sx est beaucoup plus petit que V, on tire : p = p0(1 + gSx/V).
En se limitant aux mouvements harmoniques, il vient :
md²x/dt² + p₀gS²x/V = 0.
Cette équation correspond à un mouvement harmonique de pulsation w = gS²p₀/mV.
La célérité du son dans un gaz de masse volumique m est c² = gp₀/m. (c est voisin de 340 m/s à température ambiante).
On en déduit que la fréquence propre des ondes dans la cavité est :

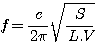
En fait, on constate que la longueur du piston à prendre en compte est L_eff = L + L₀. On démontre que le terme correctif L₀ est voisin de 8D/3p.
Un microphone placé dans la cavité délivre une tension qui est une fonction linéaire des variations de pression du gaz. Il y a résonance quand la fréquence du signal excitateur (produit par un haut parleur excité par un générateur basse fréquence) est égale à la fréquence propre du résonateur .

L'applet :

Pour réaliser la simulation, j'ai introduit (conformément à l'expérience) un amortissement visqueux.
Pour diverses valeurs de L (2cm > L < 10 cm) déterminer la valeur de la fréquence de résonance f _r.
Tracer la courbe T2 = f(L) et en déduire la valeur du terme correctif L₀.
On désigne par f⁺ et f^- les fréquences qui correspondent à une tension u égale à u_max/2^½. Déterminer Q, facteur de qualité du résonateur [Q = f _r / (f⁺ - f^-)]