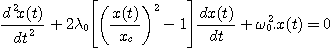Oscillateur de Van der Pol
Principe
L'amplitude des oscillations d'un oscillateur harmonique amorti diminue avec
le temps (voir le pendule de torsion). Pour obtenir
une amplitude d'oscillation constante x, il faut forcer le coefficient d'amortissement
à changer de signe lorsque l'amplitude s'écarte de la valeur xc
de la consigne choisie. Une façon d'y parvenir est d'utiliser un oscillateur
de Van der Pol qui obéit à l'équation :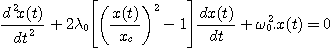
La forme retenue pour le coefficient de dx(t)/dt (le facteur d'amortissement)
permet d'atteindre le but cherché. Si ce coefficient est positif,
il y a amortissement ; quand il est négatif,
il y a amplification : le milieu
extérieur doit alors fournir de l'énergie au système.
L'équation différentielle de Van der Pol n'est pas linéaire
et n'a pas de solution analytique. Elle doit être intégrée
numériquement.
L'applet :
L'équation différentielle est intégrée par la méthode
de Runge-Kutta à l'ordre 4. Des zones de textes permettent de modifier
la valeur du coefficient d'amortissement, l'amplitude de consigne et de l'amplitude
initiale (la vitesse initiale est toujours nulle).
Un bouton permet de visualiser soit l'amplitude en fonction du temps soit le
diagramme de phase (vitesse en fonction de l'amplitude).
Pour des faibles valeurs de l'amortissement (et donc de l'amplification) le
système fonctionne en régime sinusoïdal ; l'attracteur ou
cycle limite (voir le diagramme de phase) est une ellipse. Par contre pour les
valeurs élevées de l, le signal ressemble
à des oscillations de relaxation et la forme du cycle limite se rapproche
d'un rectangle.
Dans certaines conditions, le système diverge. Le programme demande alors
de modifier les valeurs des paramètres (il faut en général
diminuer l'amortissement et l'amplitude initiale et augmenter l'amplitude de
consigne pour retrouver la convergence.
Tester par exemple l = 0,8148, Xi = 2,0, Xc = 0,9
et faire varier légèrement Xi pour apprécier la sensibilité
aux conditions initiales.
 Retour au menu "Mécanique".
Retour au menu "Mécanique".