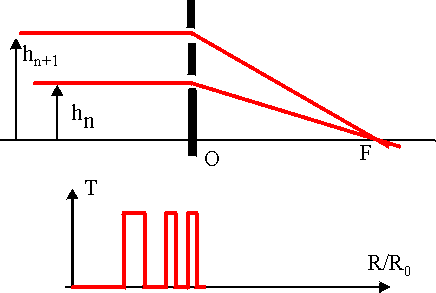
Réseau de Soret

On éclaire ce réseau avec une source monochromatique située à l'infini. Deux rayons parallèles sont diffractés lors de la traversée de deux couronnes transparentes et interfèrent au point F (OF = f) situé sur l'axe optique du système si la différence de marche est égale à un multiple de la longueur d'onde. L'amplitude transmise par chaque couronne est identique. La valeur de la différence de marche est donnée par :
d = ( f² + h_n+1²)^½ - ( f² + h_n²)^½ = kl. Si h_n << f alors d = ( h_n+1² -  h_n²)/2f.
Compte tenu de la valeur des rayons des zones, la condition d'interférence s'écrit : f = R₀²/kl.
Au point situé à l'infini, correspondent des images aux distances R₀²/l, R₀²/2l, R₀²/3l ...
Le réseau de Soret est l'équivalent d'une lentille convergente à foyers multiples. Cette lentille est entachée d'une forte aberration chromatique.
Utilisation pratique : Il faut réaliser (par photographie) une copie du réseau telle que le rayon de la couronne centrale soit de l'ordre de 1 mm. On peut utiliser le soleil comme source.
Remarque 1 : Si l'on examine dans le plan focal d'une lentille l'image donnée par un interféromètre de Fabry-Pérot, on obtient un système d'anneaux dont les rayons varient comme ceux d'un réseau de Soret.
Remarque 2 : Le réseau peut être à centre blanc ou noir ; les résultats sont identiques.
Remarque 3 : Noter l'illusion d'optique qui fait paraître plus grand le cercle central quand il est blanc.