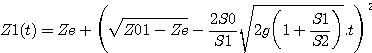
Etude du problème
On considère deux récipients cylindriques de rayons R1 et R2 (sections S1 et S2) reliés par un petit tube de rayon R0 et de section S0 contenant un liquide non visqueux. Soient Z01 et Z02 les hauteurs initiales du liquide dans les deux récipients. Comment évoluent les hauteurs de liquide en fonction du temps quand la communication est établie ?
Ce problème est le même que celui de la vidange d'un récipient avec des conditions initiales différentes.
On suppose que Z01 est supérieur à Z02. Pour traiter l'autre cas, il suffit de permuter les indices 1 et 2.
La conservation du volume de fluide permet de déterminer le niveau final (commun) Ze :
(S1 + S2).Ze = S1.Z1 + S2.Z2. (1)
Le théorème de Bernouilli permet de déterminer la vitesse du fluide dans le tube de communication :
V = [2g.(Z1 - Z2)]^½. (2)
 La variation dZ1 de Z1 pendant le temps dt est donc :
- S1.dZ1 = S0.V.dt (3).
La relation (1) permet d'exprimer dans la relation (2) Z2 en fonction de Z1 et de Ze
L'intégration de cette équation différentielle donne la loi de variation de la hauteur de liquide en fonction du temps.

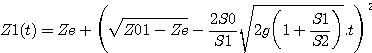
Cette relation n'est valide que si les conditions d'application du théorème de Bernouilli sont respectées. Les phénomènes sont alors indépendant de la nature du liquide.

 L'applet
Les trois zones de texte permettent de choisir les rayons des vases et celui du tube.
Pour modifier les niveaux initiaux glisser les curseurs rouge et vert avec la souris.
Pour lancer l'animation, il suffit de valider la dernière valeur entrée ou de cliquer sur le bouton [Départ].
Le chronomètre s'arrête quand le niveau d'équilibre est atteint.